
Confidence levels are represented as a percentage, for instance, the confidence level of this poll is 98%. The two terms confidence intervals and confidence levels seem alike, however, there is a difference between these two terms. Confidence Intervals Vs Confidence Levels Confidence intervals are associated with confidence levels. The confidence interval helps you to determine how confident you can be that the results from a survey reflect the opinion or trend of the entire population. These intervals are mostly accompanied by the margin of error. A researcher planning a study who wants a specified confidence level and error bound can use this formula to calculate the size of the sample needed for the study.A confidence interval reflects the extent of the uncertainty of a specific statistic. In this formula, z is, corresponding to the desired confidence level.

The formula for sample size is, found by solving the error bound formula for n. The error bound formula for a population mean when the population standard deviation is known is If researchers desire a specific margin of error, then they can use the error bound formula to calculate the required sample size. If we know that the sample mean is 68: EBM = 68.82 – 68 = 0.82.

We may know that the sample mean is 68, or perhaps our source only gave the confidence interval and did not tell us the value of the sample mean. Suppose we know that a confidence interval is (67.18, 68.82) and we want to find the error bound. You can choose the method that is easier to use with the information you know. Notice that there are two methods to perform each calculation.
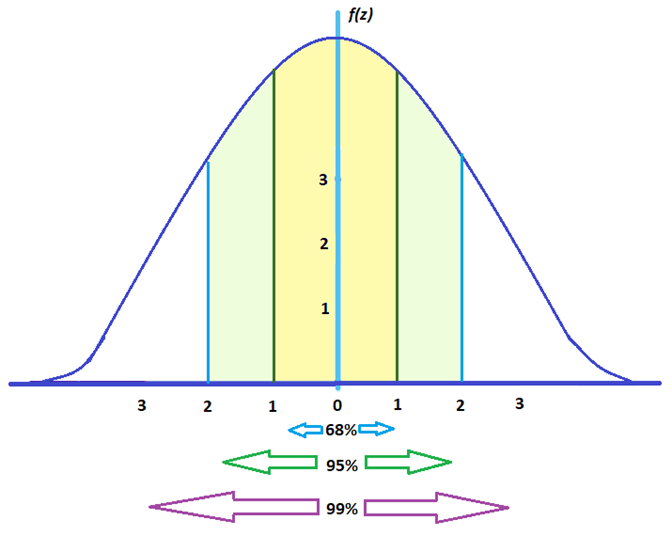
OR, average the upper and lower endpoints of the confidence interval. Subtract the error bound from the upper value of the confidence interval,. OR, from the upper value for the interval, subtract the lower value. From the upper value for the interval, subtract the sample mean,. If we know the confidence interval, we can work backwards to find both the error bound and the sample mean. However, sometimes when we read statistical studies, the study may state the confidence interval only. When we calculate a confidence interval, we find the sample mean, calculate the error bound, and use them to calculate the confidence interval. Working Backwards to Find the Error Bound or Sample Mean Decreasing the confidence level decreases the error bound, making the confidence interval narrower. Increasing the confidence level increases the error bound, making the confidence interval wider. Summary: Effect of Changing the Confidence Level To be more confident that the confidence interval actually does contain the true value of the population mean for all statistics exam scores, the confidence interval necessarily needs to be wider. If you look at the graphs, because the area 0.95 is larger than the area 0.90, it makes sense that the 95% confidence interval is wider. In Example 4, the 95% confidence interval is (67.02, 68.98). In Example 2, the 90% confidence interval is (67.18, 68.82). We estimate with 95% confidence that the true population mean for all statistics exam scores is between 67.02 and 68.98.ĩ5% of all confidence intervals constructed in this way contain the true value of the population mean statistics exam score. This can also be found using appropriate commands on other calculators, using a computer, or using a probability table for the standard normal distribution. The area to the right of z 0.025 is 0.025 and the area to the left of z 0.025 is 1 – 0.025 = 0.975.







 0 kommentar(er)
0 kommentar(er)
